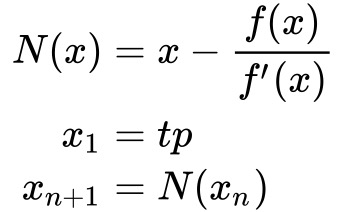This page is for explorations in 3D Newton fractals. Newton's method is normally used for solving for roots of equations. Newton's method does not seem to work correctly with triplex numbers but it does generate really nice fractals.
The formula for Newton's method is shown below.
The formula is initialized with an initial guess like a Julia fractal and is iterated. Any part of the model that is visible is an initial guess that converges to a number (not a root unfortunately). The bailout value is critical to making an interesting fractal. If the bailout is too high, all numbers will converge and the fractal will be a sphere. The sphere has voids that can be explored but a better approach is to start with a bailout near 1 to have a fractal that has visible structure without cutting it open.
Further investigation has revealed that the algorithm converges to a number that is not a root of the equation. It appears that this is a fundamental problem with the current definition of triplex numbers. If any further revelations come to light they will be discussed here.
The resulting formula must stay within the limitations of Fracton's triplex language. The biggest issue is requiring multiply and divide to have at least one component that is a scalar number. Here is a table of the equations that appear in the fractals below.
| Fracton Equation | f(x) | Newton's Method |
| f = f - 0.2 * (f - f^-4) | z^5-1 | x_{n+1} = x - \frac{x^5-1}{ 5x^4} = x - \frac{x-x^{-4}}{ 5} |
| f = f - 1 / (5 * f^-1 + 2 * f^-4) - 1 / (5 * f^2 + 2 * f^-1) + 2 / (5 * f^4 + 2 * f) |
x^5 + x^2 - 2 | x_{n+1} = x - \frac{x^5+x^2-2}{ 5x^4+2x}>
= x - \frac{x^5}{ 5x^4+2x} - \frac{x^2}{ 5x^4+2x} + \frac{2}{ 5x^4+2x} = x - \frac{1}{ 5x^{-1}+2x^{-4}} - \frac{1}{ 5x^2+2x^{-1}} + \frac{2}{ 5x^4+2x} |
You can download a folder of files to generate the fractals.
Download Fracton document files newton3d.zip
- This page uses cookies but you can still view the page with all cookies turned off..
- Posting requires a Disqus account and cookies have to be enabled. See Posting FAQ and Guidelines
- This discussion is moderated.
- Click on an image to open it in a new window at full size.
- Right click an image to download the full size image to your computer.